[프로그래머스] Lv1. 두 정수 사이의 합

July 17, 2021 1 분 소요

두 정수 a, b가 주어졌을 때 a와 b 사이에 속한 모든 정수의 합을 리턴하는 함수, solution을 완성하세요.예를 들어 a = 3, b = 5인 경우, 3 + 4 + 5 = 12이므로 12를 리턴합니다.

제한 조건

def solution(a, b):
    answer = 0
    if a > b:
        a, b = b, a
    for i in range(a, b+1):
        answer += i
    return answer

for문과 range를 사용해서 풀 수 있는 아주 기초적인 문제였다. 다만, a, b 의 대소관계가 정해져 있지 않기 때문에 a의 값이 b보다 클 경우 두 값의 위치를 바꿔주는 코드가 포함되었다.

프로그래머스를 통해 풀어본 첫번째 알고리즘 연습문제.

아주 간단하다고만 생각했는데 다른 사람들의 풀이를 보고 충격을 받게 되었다…

def solution(a, b):
    if a > b: a, b = b, a
    return sum(range(a,b+1))

사실 sum 함수를 써도 되는 문제였다…

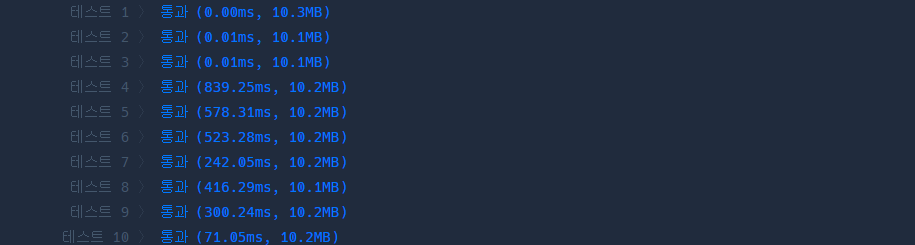
for 문을 써서 코드를 작성했을 때는 아무래도 if 문을 1번 실행하고, for문의 판단을 a와 b 사이의 숫자 갯수만큼 n번 그리고 덧셈을 또 n번, 총 2n+1 만큼 실행해줘야하기 때문에 실행복잡도가 O(n) 이 되어 아래와같이 나왔다.

테스트 1, 2, 3은 아마도 숫자가 작았는지 문제가 없어 보이지만 테스트 4 부터는 실행시간이 급격히 늘어났음을 확인할 수 있다.

그런데 sum 함수를 사용해서 문제를 풀 경우 시간복잡도는 똑같이 O(n)이지만 실행시간은 300ms 대로 많이 줄어들었음을 확인할 수 있었다.

첫번째 풀이가 ‘아 sum을 써도 되는데 왜 안썼지?’ 정도의 깨달음이었다면, 정말 충격적인건 바로 아래의 코드였다.

def solution(a, b):
    return (abs(a-b)+1)*(a+b)//2

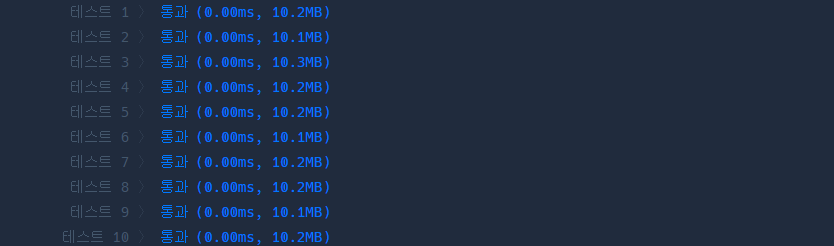
절대값과 n(n+1)/2 수열 공식을 사용한 풀이로, 이렇게 했을 경우 시간복잡도가 O(1)으로 확연하게 줄어들게 된다. 무려 실행시간 0.00ms ㄷㄷ…

물론 아직 기초를 배우는 단계이기는 하지만, 모든 교재나 강의가 for문을 사용한 방법만을 알려주고 있을 때 수학적 지식을 알고리즘에 적용하면 이런 코드를 손쉽게 작성할 수 있다는 충격을 알고리즘 연습을 위해 풀어본 가장 첫번째 문제부터 받게 되었다…

블로그 이전