[CS50] 4.알고리즘, Algorithm (1)

검색 알고리즘

지난 챕터에서 메모리에 자료를 저장하는 방식으로 배열이라는 자료구조(Data Structure)가 사용된다는 것을 알 수 있었다.

배열에는 상,하,좌,우 칸 별로 위치 혹은 순서의 개념이 존재하는데, 만약 이런 배열 안에서 특정 값을 찾고 싶은 경우 이론적으로 어떤 방법을 사용할 수 있을까?

선형 검색 (Linear Search)

배열의 인덱스를 처음부터 끝까지 하나씩 증가시키면서 방문하여 찾는 값이 속해있는지를 검사한다.

모든 인덱스를 확인하기 때문에 정확도는 좋지만 효율성은 떨어질 수 있다. 하지만 어떤 값들이 어떤식으로 정렬되어 있는지 확인할 수 없는 상황에서는 선형 검색을 진행하는 것이 최선일 수 있다.

이진 검색 (Binary Search)

만약 배열이 정렬되어 있다면, 배열 중간의 인덱스부터 시작해서 찾고자 하는 값과 비교하며 그보다 작거나 큰 값이 저장되어 있는 방향의 인덱스로 이동을 반복하며 검색을 진행할 수 있다.

알고리즘 표기법

The Big-O Notation

Big-O 표기법은 알고리즘이 얼마나 잘 설계되었는지(효율적인지)를 설명하기 위한 방법의 하나이며 O는 “on the Order of”의 약자로, 문제해결에 걸리는 시간이 얼마나 커지는지를 간단하게 설명한다.

아래 사진은 선형 검색과 이진 검색을 했을 때 문제의 크기에 따라 문제해결에 걸리는 시간이 어떻게 증가하는지를 나타낸 그래프인데, 일반 선형 검색을 했을 때의 식을 n, 동시에 두 개씩 작업을 진행하는 선형 검색을 했을 때의 식이 n/2, 그리고 이진 검색을 했을 때의 식이 log₂n 로 표기되어 있다.

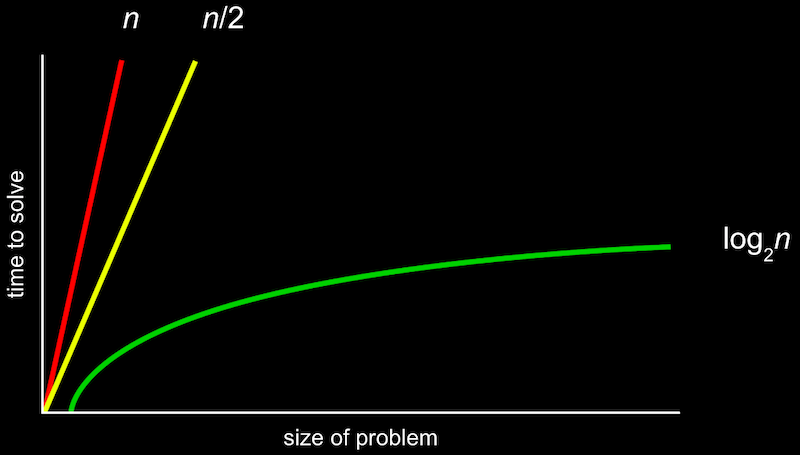
이 때 시간이 n, n/2, log₂n 만큼 소요된다고 표현하기 보다는 “해당 알고리즘의 실행 시간은 O(n)이다 (on the order of n)” 와 같은 방식으로 n을 기준으로 하는 추정치를 표현한다.

여기에서 n의 크기가 커질수록 계수나 상수가 미치는 영향은 큰 의미가 없어지기 때문에 n과 n/2 모두 O(n) 으로 표기한다.

이 외에도 아래 목록과 같은 Big-O 표기가 많이 사용되는데, 목록 위에서 아래로 내려갈수록 소요되는 시간 또는 단계가 줄어든다.

• O(n²)
• O(n log n)
• O(n) - 선형 검색
• O(log n) - 이진 검색
• O(1)

The Big-Ω Notation

Big-O 표기법은 실행 시간의 상한, 즉 걸릴 수 있는 최대의 시간(최악의 경우)을 나타낸 것이라면 Big-Ω 표기법은 이와 반대로 실행 시간의 하한, 즉 걸릴 수 있는 최소 시간(최선의 경우)를 나타낸다.

n개의 항목이 있을 때 최대 n번의 검색을 해야하는 선형 검색은 상한이 O(n)이지만, 운이 좋을 경우 한 번에 검색을 끝낼 수도 있으므로 하한을 Ω(1)이 된다. 그리고 이진 검색 또한 운이 좋을 경우 한 번에 검색을 끝낼 수 있기 때문에 마찬가지로 하한은 Ω(1)이 된다.

Big-Ω 표기 예는 다음과 같으며, 마찬가지로 목록 위에서 아래로 내려갈수록 소요되는 시간 또는 단계가 줄어든다.

• Ω(n²)
• Ω(n log n)
• Ω(n) - 예) 배열 안에 존재하는 값의 개수 세기
• Ω(log n)
• Ω(1) - 선형 검색, 이진 검색

이로써 Big-O 와 Big-Ω 를 사용하여 코드나 알고리즘이 주어지는 입력값에 따라 얼마나 좋은지 파악할 수 있다.

추가로, Big-O와 Big-Ω 중 Big-O 가 좋아야 더 좋은 알고리즘이라고 할 수 있는데 프로그래밍을 할 때는 최선의 경우에 얼마나 잘 작동하는지보다 최악의 경우 또는 평균적으로 얼마나 잘 작동하는지를 더 유의하는 것이 좋기 때문이다.

정렬

선형검색과 이진검색을 비교했을 때는 이진검색을 사용하는 것이 더 효율적이다. 그러나 그건 배열이 정렬이 되어 있는 경우에만 해당하는데, 그렇다면 정렬되지 않은 배열이 있는 경우 배열을 먼저 정렬하고 이진검색을 하는 것이 더 효율적일까?

버블 정렬 (Bubble Sort)

버블 정렬은 두 개의 인접한 자료 값을 비교하면서 위치를 교환하는 방식으로 정렬하는 방법이다. 마치 큰 버블일 수록 더 위쪽으로 떠오르는 것과 유사하기 때문인데, 의사 코드로 나타낸다면 다음과 같다.

Repeat n-1 times:  #n개의 값이 있을 때 인접한 값끼리 비교할 수 있는 경우는 n-1번 존재
	for i from 0 to n-2: #0번 자리부터 끝에서 두번째 자리까지
		if i'th and i+1th elements are out of order #i번째 자리와 그 옆의 값이 정렬이 안되어있다면
		swap places  #위치를 바꿔라

그리고 이 알고리즘을 수학 공식으로 바꿀 경우, 바깥쪽 반복문은 n-1회 반복하고, 안쪽 반복문또한 0번부터 n-2번까지 n-1회 반복하므로 (n-1) x (n-1) 이 된다.

곱하면 n²-2n+1 이 되는데, 지수가 가장 큰 부분의 영향력이 가장 크기 때문에 버블 정렬의 실행 시간 상한은 O(n²) 라고 할 수 있다.

또한 버블 정렬을 하는데 최소 시간이 걸리는 경우는 이미 정렬이 되어있는 경우인데, 이 때도 정렬여부와 상관없이 루프를 돌며 값을 비교해야하기 때문에 실행 시간의 하한도 Ω(n²)가 된다.

결국 버블 정렬을 사용할 경우 이진 검색(O(log n))을 사용하더라도 정렬 과정이 O(n²) 이기 때문에 O(n)인 선형검색보다 더 오랜 시간이 걸리게 된다.

선택 정렬 (Selection Sort)

선택 정렬은 배열 안의 자료 중 가장 작을 수를 찾아 첫 번째 위치의 수와 교환해주는 방식의 정렬이다. 선택 정렬은 교환 횟수를 최소화하는 반면 각 자료를 비교하는 횟수는 증가한다.

의사 코드로 적으면 다음과 같다.

For i from 0 to n–1: #0번부터 n-1번까지 반복
    Find smallest item between i'th item and last item
		#현재 자리(i)부터 마지막 번호까지 확인하여 가장 작은 수를 찾은 뒤
    Swap smallest item with i'th item
		#현재 자리(i)의 수와 가장 작은 수를 교환한다 

알고리즘을 수학 공식으로 바꿀 경우:

• (n-1)+(n-2)+(n-3)+…+2+1

• (n-1)+1+(n-2)+2+…

• n+n+n+n+…

• 즉, n-1 개의 값이 있고, (n-1+1)과 같은 경우가 짝을 이뤄 총 (n-1)/2 회 존재한다. n이 (n-1)/2 번 있는 것이므로 최종 값은 n(n-1)/2

  ⇒ O(n²)

선택 정렬도 버블 정렬과 마찬가지로 최선의 경우에도 값을 모두 비교하기 때문에 Ω(n²). 결국 소요 시간의 상한과 하한 모두 버블 정렬과 동일하다.