OpenCV - 에지 검출
에지 검출
에지(edge): 한쪽 방향으로 픽셀 값이 급격하게 바뀌는 부분
사람의 눈으로도 테두리를 인식하는 것은 중요하다. 같은 색, 밝기가 섞여있을 경우 사물을 구분하기 어려운 경우가 많은데, 색이나 밝기가 급격하게 변하는 부분이 있을 때 사물의 구분이 쉬워진다.
마찬가지로 컴퓨터로 영상을 인식할 때도 색이나 밝기값이 변하는 부분을 기준으로 테두리를 검출해주면 사물을 인식하기가 쉬워지고 방향성 탐지에 도움이 된다. **
에지 검출의 원리: 미분과 그래디언트
영상에서 에지를 찾아내려면 픽셀 값의 변화율을 측정해서 변화율이 큰 픽셀을 선택해야 한다. 픽셀값의 변화율은 수학에서 주어진 함수의 순간 변화율인 미분(derviative)을 구하여 미분 값이 0보다 훨씬 크거나 훨씬 작은 위치를 찾으면 된다.
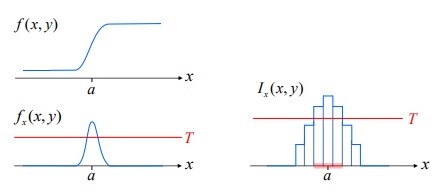
문제는 영상은 픽셀로 이루어져있기 때문에 일반적인 수학 함수처럼 값이 연속적이지 않고, x방향과 y방향 모두 계산해야하는 2차원이라는 점이다.
실수처럼 연속적인 값 대신 영상과 같이 정수단위 좌표에 픽셀이 나열된 형태의 함수를 이산함수라고 한다. 우선 1차원 이산함수의 미분을 구하려면 미분 근사화라는 것을 해야하는데 미분 근사는 다음과 같이 전진 차분, 후진 차분, 중앙 차분 세 가지 방법을 주로 이용한다.
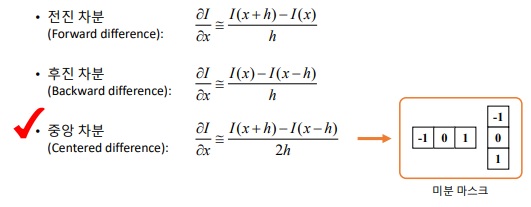
I(x)가 1차원 이산함수고, h가 픽셀의 간격이라고 할 때, 전진차분은 자기 바로 앞에 있는 픽셀에서 자기 자신의 픽셀 값을 뺀 형태고 후진 차분은 반대로 뒤에 있는 픽셀에서 자신의 픽셀 값을 뺀 형태다. 중앙 차분은 자신을 제외하고 앞뒤에 있는 픽셀값을 이용하는 방법인데, 중앙 차분이 가장 이론적으로 오류가 적고 실제 영상 미분에 널리 사용된다.
이제 2차원 영상에 대한 미분 방법을 찾으면 되는데, 방법은 x축 방향과 y축 방향으로 각각 미분을 한 뒤 두 결과를 합치는 것이다. 한쪽 방향만으로의 미분을 편미분(partial derivative)이라고 하며 편미분은 위 그림의 가로와 세로 미분 마스크를 각각 사용한 마스크 연산을 통해 구할 수 있다.
다음, 각 x축과 y축 편미분을 한꺼번에 벡터로 표현하면 되는데 이것을 그래디언트(gradient)라고 부른다. 그래디언트는 벡터이기 때문에 크기(magnitude)와 방향(phase) 성분을 가지고 있으며 크기는 변화율의 세기, 방향은 변화 정도가 가장 큰 방향을 나타낸다.
이렇게 만들어진 결과물, 그래디언트에서 에지를 찾는 방법은 그래디언트 크기가 특정 값보다 큰 위치를 찾는 것인데, 이 때 에지 여부를 판단하기 위해 기준이 되는 값을 임계값(threshold)라고 한다. 임계값은 보통 사용자의 경험에 의해 결정되며 높게 설정할 수록 밝기 차이가 급격하게 변하는 에지 픽셀만 검출되고 낮을 수록 약한 에지도 검출된다.
마스크 기반 에지 검출
앞서 편미분을 구할 때 마스크 연산을 한다고 했다. 하지만 실제 영상에서는 잡음이 포함되어 있어 1x3 또는 3x1 크기의 마스크를 이용하여 미분을 구하면 부정확한 결과가 생성될 수 있다. 그래서 실제로는 조금 더 큰 크기의 미분 근사 마스크를 사용한다.
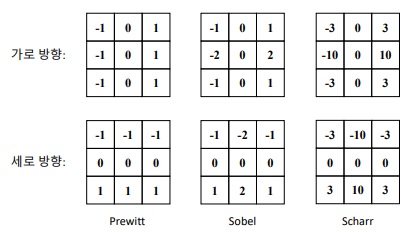
소벨 필터 (Sobel filter)
가장 널리 사용되는 미분 마스크로 OpenCV에서 소벨 필터를 사용하는 함수 Sobel()을 통해 영상을 미분하고 에지를 검출할 수 있다.
cv2.Sobel(src, ddepth, dx, dy, ksize=None, scale=None, delta=None, borderType=None)
- ddepth: 결과 영상 데이터 타입, -1이면 입력 영상과 동일.
- dx: x방향 미분 차수
- dy: y방향 미분 차수
- ksize: 커널 크기. 보통 3
- scale: 결과 영상에 추가로 곱할 값. 기본은 1.
- delta: 결과 영상에 추가로 더할 값. 기본은 0.
src = cv2.imread('c.jpg', cv2.IMREAD_GRAYSCALE)
dx = cv2.Sobel(src, -1, 1, 0, delta=128)
dy = cv2.Sobel(src, -1, 0, 1, delta=128)
cv2.imshow('src', src)
cv2.imshow('dx', dx)
cv2.imshow('dy', dy)
cv2.waitKey(0)
cv2.destroyAllWindows()

샤르 필터 (Scharr filter)
2000년대에 나온 마스크 종류로(소벨은 70년대), 커널의 중심에서 멀어질수록 정확도가 떨어지는 소벨 필터의 단점을 보완하여 더 정확한 미분계산을 한다. 하지만 소벨 필터가 직관적이라는 이유로 더 많이 사용된다고 한다. Scharr() 함수를 이용해서 미분을 구할 수 있다.
cv2.Scharr(src, ddepth, dx, dy, scale=None, delta=None, borderType=None)
- ddepth: 결과 영상 데이터 타입, -1이면 입력 영상과 동일.
- dx: x방향 미분 차수
- dy: y방향 미분 차수
- scale: 결과 영상에 추가로 곱할 값. 기본은 1.
- delta: 결과 영상에 추가로 더할 값. 기본은 0.
src = cv2.imread('c.jpg', cv2.IMREAD_GRAYSCALE)
dx = cv2.Scharr(src, -1, 1, 0, delta=128)
dy = cv2.Scharr(src, -1, 0, 1, delta=128)
cv2.imshow('src', src)
cv2.imshow('dx', dx)
cv2.imshow('dy', dy)
cv2.waitKey(0)
cv2.destroyAllWindows()

Sobel() 함수의 ksize 인자에 FILTER_SCHARR 또는 -1을 지정해도 샤르 마스크를 사용할 수 있다.
그래디언트 계산
소벨 필터 또는 샤르 필터 함수를 사용해서는 x와 y 편미분만 구할 수 있었다. 이제 미분 값으로 그래디언트 크기를 계산하고 임계값을 기준으로 정리하여 에지를 검출할 수 있다.
그래디언트 크기는 magnitude() 함수를 사용하고, 만약 그래디언트 방향을 계산하고 싶다면 phase() 함수를 사용할 수 있다.
cv2.magnitude(x, y)
- x: x축 미분값 (실수형*)
- y: y축 미분값 (실수형*)
- *입력하는 x, y 값은 CV_32F 또는 CV_64F 타입의 행렬 또는 벡터여야 한다.
cv2.phase(x, y, angleInDegree=None)
- x: x축 미분값(실수형)
- y: y축 미분값(실수형)
- angleInDegree: True이면 각도, False이면 래디언
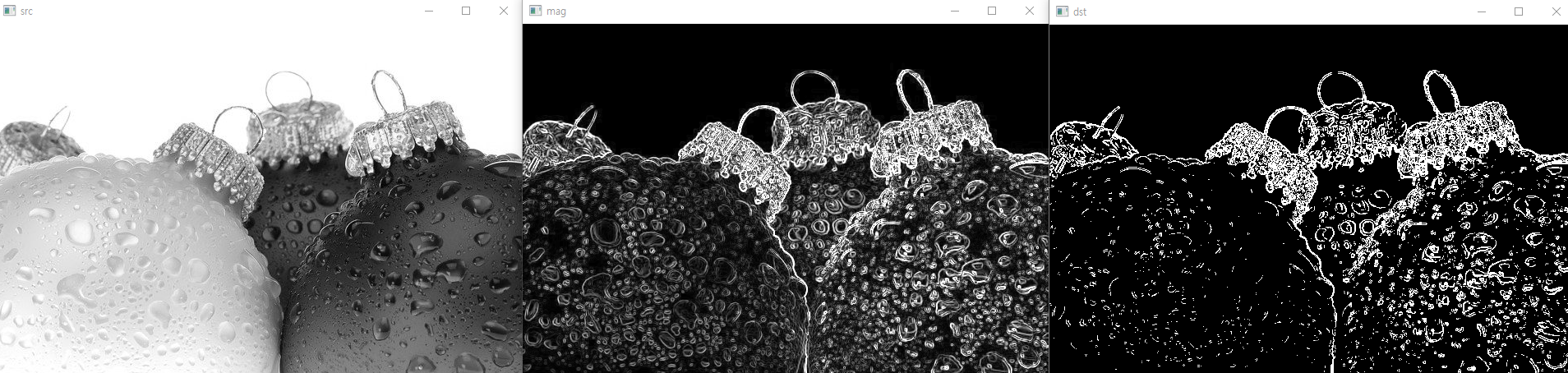
src = cv2.imread('c.jpg', cv2.IMREAD_GRAYSCALE)
dx = cv2.Sobel(src, cv2.CV_32F, 1, 0)
dy = cv2.Sobel(src, cv2.CV_32F, 0, 1)
mag = cv2.magnitude(dx, dy)
mag = np.clip(mag, 0, 255).astype(np.uint8) # 이미지 출력을 위해 다시 그레이스케일 형식으로 변경
dst = np.zeros(src.shape[:2], np.uint8)
dst[mag > 128] = 255
#_, dst = cv2.threshold(mag, 120, 255, cv2.THRESH_BINARY) # 뒤에 배울 이진화 함수 사용 예
cv2.imshow('src', src)
cv2.imshow('mag', mag)
cv2.imshow('dst', dst)
cv2.waitKey()
cv2.destroyAllWindows()
캐니 에지 검출
소벨 마스크 기반 에지 검출은 구현이 간단하고 빠르지만 그래디언트 크기만을 기준으로 에지 픽셀을 검출하기 때문에 임계값에 민감하고 에지 픽셀이 두껍게 표현되는 문제가 있다. 그래서 좋은 에지 검출을 위해 캐니(J. Canny)는 다음 조건들을 제시하였다.
- 정확한 검출 (good detection): 점이나 노이즈를 에지로 찾거나 에지를 놓치는 확률 최소화
- 정확한 위치 (good localization): 실제 에지의 중심을 검출
- 단일 에지 (single edge): 하나의 에지는 하나의 점으로 표현
그리고 위 조건을 모두 만족하는 에지 검출 방법으로 캐니 에지 검출기(canny edge detector)를 제시했다.
캐니 에지 검출기는 그래디언트의 크기 및 방향을 모두 고려하고, 서로 연결되어 있는 가능성이 높은 점을 고려해서 그래디언트 크기가 다소 약하게 나타나는 에지도 놓치지 않고 찾는다. 그 검출 단계는 다음과 같다.
- 가우시안 필터링: 영상에 포함된 잡음 제거
- 그래디언트 계산: 소벨 마스크를 이용해서 그래디언트 크기, 방향 계산
- 비최대 억제: 하나의 에지가 여러 개의 픽셀로 표현되는 것을 막기 위해 그래디언트 크기가 단순히 임계값보다 큰 픽셀을 선택하지 않는 비최대 억제(non-maximum suppression)를 사용, 그래디언트 크기가 국지적 최대(local maximum)인 픽셀만을 선택.
- 히스테리시스 에지 트래킹 (hysteresis edge tracking): 이중 임계값(낮은 임계값 & 높은 임계값)을 사용해서 걸러진 에지 중 높은 임계값과 낮은 임계값 사이의 약한 에지는 버리고 높은 임계값보다 큰 강한 에지와 연결된 에지만 최종 선택
위 과정을 자동으로 처리하는 Canny() 함수를 사용하여 캐니 에지 검출이 가능하다.
cv2.Canny(img, threshold1, threshold2, apertureSiz=None, L2gradient=None)
- threshold1 – Hysteresis Thredsholding 작업에서의 min (낮은임계값)
- threshold2 – Hysteresis Thredsholding 작업에서의 max (높은임계값)
- apertureSiz - 소벨 연산에 사용할 커널 크기
- L2gradient - 그래디언트 계산 수식 지정. True, False(기본값)
src = cv2.imread('building.jpg', cv2.IMREAD_GRAYSCALE)
dst = cv2.Canny(src, 50, 150)
cv2.imshow('src', src)
cv2.imshow('dst', dst)
cv2.waitKey()
cv2.destroyAllWindows()

허프 변환 직선 검출
직선은 영상에서 찾을 수 있는 많은 특징 중의 하나이며 중요한 정보를 제공한다. 자율주행차가 차선을 검출하는 용도로 사용될 수도 있고, 영상의 수평선 또는 수직선 성분을 찾아내어 자동 영상 회전을 위한 정보로도 사용할 수 있다.
영상에서 직선을 찾기 위해서는 우선 에지를 찾아내고, 에지 픽셀들이 일직선상에 배열되어 있는지를 확인해야 한다.
허프 변환 (Hough transform)
허프 변환은 2차원 xy좌표에서 직선의 방정식을 파라미터 공간으로 변환하여 직선을 찾는 알고리즘이다.
기울기 a와 y절편 b를 갖는 직선의 방정식은 y = ax + b 인데, 이 수식은 b = -xa+y 로도 바꿔 쓸 수 있다. 이 때, x와 y를 축으로 갖는 xy공간에서 y = ax + b 직선의 아무점 (x₁, y₁)을 선택하고 이 좌표로 a와 b를 축으로 갖는 ab 공간에서 직선 b = -x₁a + y₁ 를 만들고 다른 (x, y) 좌표로도 ab공간에서 직선을 만들면 모두 (a, b) 점에서 교차를 하게 된다.
이 사실을 이용하여 xy 축으로 이루어진 영상에서 에지로 판별된 모든 점들을 찾아 ab 공간에 직선을 만들면 직선이 많이 교차되는 특정 (a, b) 좌표들이 생기고, 그 특정 좌표의 a, b 값을 이용하면 영상 속 직선 y = ax + b 를 찾을 수 있게 된다.
하지만, y = ax + b 방정식은 y축과 평행한 수직선 등 모든 형태의 직선을 표현하기 어렵다. 그래서 실제 허프 변환을 구현할 때에는 극좌표계 직선의 방정식을 사용하고 파라미터 공간에서 직선 대신 곡선을 그려서 구현한다.

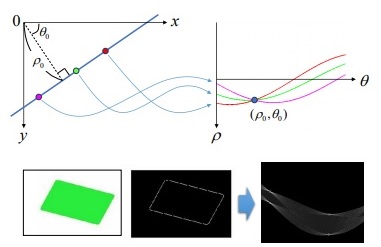
코드로는 HoughLines() 함수를 사용하여 허프 변환 직선 검출을 할 수 있다.
cv2.HoughLines(img, rho, theta, threshold, srn=None, stn=None, min_theta=None, max_theta=None)
- rho – r 값의 범위 (0 ~ 1 실수)
- theta – 𝜃 값의 범위(0 ~ 180 정수)
- threshold – 직선으로 판단할 임계값, 숫자가 작으면 많은 선이 검출되지만 정확도가 떨어지고, 숫자가 크면 정확도가 올라감.
- srn, stn - 멀티 스케일 허프 변환에서 rho, theta를 나누는 값. 기본은 0
- min_theta, max_theta - theta 최소, 최대값
그런데 HoughLines() 함수는 반환된 모든 점의 기울기를 계산해서 시작점과 끝점을 계산해야 하고 모든 점에 대해서 연산을 진행하기 때문에 속도가 느리다. 이를 보완하기 위해 확률 허프 변환 함수 HoughLinesP()를 사용한다.
확률 허프 변환은 허프 변환을 최적화 한 것으로, 모든 점을 대상으로 하지 않고 임의의 점을 이용해서 직전을 찾는다. 그리고 rho와 theta 대신 직선의 시작점과 끝점 좌표를 반환해주기 때문에 쉽게 화면에 표현이 가능하다.
cv2.HoughLinesP(image, rho, theta, threshold, minLineLength, maxLineGap)
- rho – r 값의 범위 (0 ~ 1 실수)
- theta – 𝜃 값의 범위(0 ~ 180 정수)
- threshold – 직선으로 판단할 임계값
- minLineLength - 검출할 선의 최소 길이
- maxLineGap - 직선으로 간주할 최대 에지 점 간격
src = cv2.imread('building.jpg', cv2.IMREAD_GRAYSCALE)
edges = cv2.Canny(src, 50, 150)
lines = cv2.HoughLinesP(edges, 1, np.pi / 180., 160,
minLineLength=50, maxLineGap=5)
dst = cv2.cvtColor(edges, cv2.COLOR_GRAY2BGR)
if lines is not None:
for i in range(lines.shape[0]):
pt1 = (lines[i][0][0], lines[i][0][1]) # 시작점 좌표
pt2 = (lines[i][0][2], lines[i][0][3]) # 끝점 좌표
cv2.line(dst, pt1, pt2, (0, 0, 255), 2, cv2.LINE_AA)
cv2.imshow('src', src)
cv2.imshow('dst', dst)
cv2.waitKey()
cv2.destroyAllWindows()

허프 변환 원 검출
중심좌표가 (a, b)이고 반지름이 r인 원의 방정식은 (x-a)² + (y-b)² = r² 로 표현한다. 하지만 이 경우 파라미터가 a, b, r 세 개로, 허프 변환을 그대로 적용하려면 3차원 파라미타 공간을 사용해야하고 너무 많은 메모리와 연산시간을 필요로 한다.
그래서 OpenCV에서는 영상에 존재하는 모든 원의 중심 좌표를 찾고, 검출된 원의 중심으로부터 원에 적합한 반지름을 구하는 허프 그래디언트 방법(Hough gradient method)를 사용해서 원을 검출한다. HoughCircles() 함수를 사용하면 된다.
cv2.HoughCircles(img, method, dp, minDist, param1=None, param2=None, minRadius=None, maxRadius=None)
- method: cv2.HOUGH_GRADIENT 만 가능
- dp: img와 축적배열 크기 비율. 1은 같음, 2는 축적배열이 img의 반
- minDist: 검출된 원 중심점들의 최소 거리
- param1: 케니 검출기의 높은 임계값
- param2: 축적 배열의 원 검출을 위한 임계값
- minRadius, maxRadius: 검출할 원의 최소, 최대 반지름
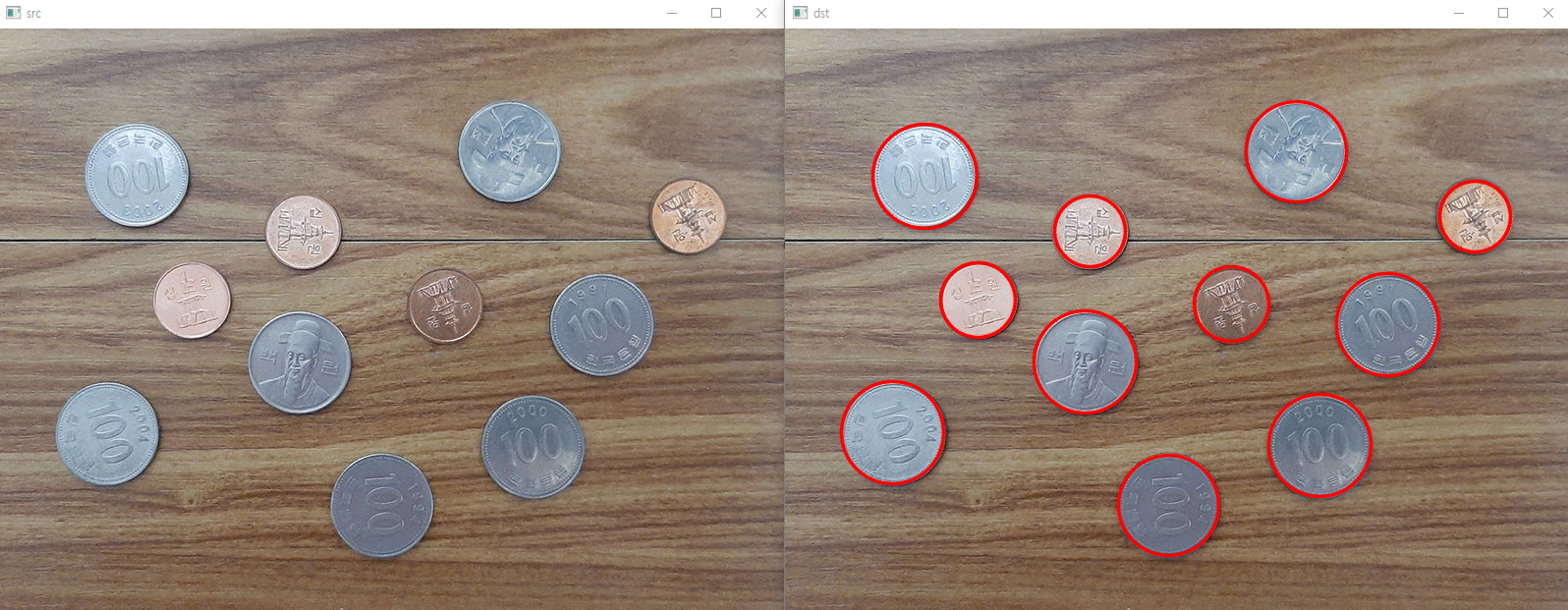
src = cv2.imread('coins1.jpg')
gray = cv2.cvtColor(src, cv2.COLOR_BGR2GRAY)
blr = cv2.GaussianBlur(gray, (0, 0), 1.0)
circles = cv2.HoughCircles(blr, cv2.HOUGH_GRADIENT, 1, 50,
param1=150, param2=40, minRadius=20, maxRadius=80)
dst = src.copy()
if circles is not None:
for i in range(circles.shape[1]):
cx, cy, radius = circles[0][i]
cv2.circle(dst, (int(cx), int(cy)), int(radius), (0, 0, 255), 2, cv2.LINE_AA)
#cv2.circle(이미지, 중심점, 반지름,색상,두께), LINE_AA = 부드러운 커브를 위해 앤티 앨리어싱 된 선
cv2.imshow('src', src)
cv2.imshow('dst', dst)
cv2.waitKey()
cv2.destroyAllWindows()

댓글남기기